Tag: SPY
Why are overnight periods riskier? For one, you can’t use stops to limit your risk. But more importantly, the distribution of overnight returns has far more extreme negative returns than the intraday or close-to-close periods. Let’s take a look at some stats on close-to-open, open-to-close, and close-to-close returns for SPY:

Some definitions:
- Skew: negative skew means longer tails on the negative side.
- Kurtosis: higher kurtosis means heavier tails (the normal distribution has a kurtosis of 3).
First of all, overnight returns are not that volatile. But per-unit-volatility, they are far riskier due to the higher frequency of extreme returns. I calculated the magnitude of returns in terms of standard deviations (based on 10-day realized volatility), and overnight returns have a 5 standard deviation move more than twice as frequently as close-to-close returns. You can expect a 5SD overnight move about once a year.
Here’s a histogram of close-to-close returns and close-to-open returns. You can clearly spot the skewness around the -6% to -3% area. The value on the far left is from Oct 24 2008. Also note that just because the skewness is negative doesn’t mean that short positions are safe: the tails of the overnight returns are heavy on the right side as well.

Close-to-open returns were adjusted to have the same volatility as the close-to-close returns to make the comparison a bit easier
Market Regimes
These risks are about the same in bull and bear markets. On the other hand they seem to be smaller in high-volatility environments (possibly a side-effect of mean-reverting volatility). When SPY’s 20-day realized volatility is above 20%, the tail risks of overnight returns are about the same as those of close-to-close returns. But this isn’t all that helpful, because after all in times of high volatility your position sizing is already limited.

The Weekend
The weekend is a special case of even higher risk; you can’t treat it like other overnight periods. It’s more volatile, and features even more frequent extreme losses. In my own position sizing I always put additional limits on trades over the weekend.

Concluding Thoughts
Different instruments behave in different ways, especially when it comes to different asset classes. Overnight dangers tend to be relatively larger for stocks compared to indices. So make sure that your sizing is adapted to the unique characteristics of the instruments that you’re trading.
As a rule of thumb I’d say that given an equal volatility exposure, overnight returns expose you to about ~1.5-2x risk of extreme negative returns, while the weekend exposes you to 2-2.5x risk of extreme negative returns. But does this mean that you should halve any overnight trades that you enter on Fridays? Not necessarily. There is no perfect answer to this dilemma: different traders and different strategies will have different views on how much they are willing to trade returns for less extreme moves. The important part is to quantify the trade-off so that you know exactly how much you’re giving up and how much risk you’re taking on.
Read more Overnight Risk
And now for something completely different. A bit of macro and a bit of factor relative performance: what happens when yield spreads and small caps diverge from the S&P 500?
High Yield Spreads
First, let’s play with some macro-style data. Below you’ll find the SPY and BofA Merrill Lynch US High Yield Master II Option-Adjusted Spread (a high yield bond spread index) plotted against SPY.
Obviously the two are inversely correlated as spreads tend to widen in bear markets. Very low values are a sign of overheating. We’re still about 130 bp away from the pre-crisis lows, so in that regard the current situation seems pretty good. There’s a bit more to it than that, though.
First, divergences. When stocks keep making new highs and spreads start rising, it’s generally bad news. Some of the most interesting areas to look at are July ’98, April ’00, July ’07, and July ’11.
Also interesting is the counter-case of May ’10 which featured no such divergence: the Flash Crash may have been the driver of that dip, and that’s obviously unconnected to the macro situation in general and high yield spreads in particular.
So, let’s try to quantify these divergences and see if we can get anything useful out of them…on the chart above I have marked the times when both the spread and SPY were in the top 10% of their 100-day range. As you can see, these were generally times close to the top, though there were multiple “false signals”, for example in November ’05 and September ’06. Here are the cumulative returns for the next 50 days after such a signal:
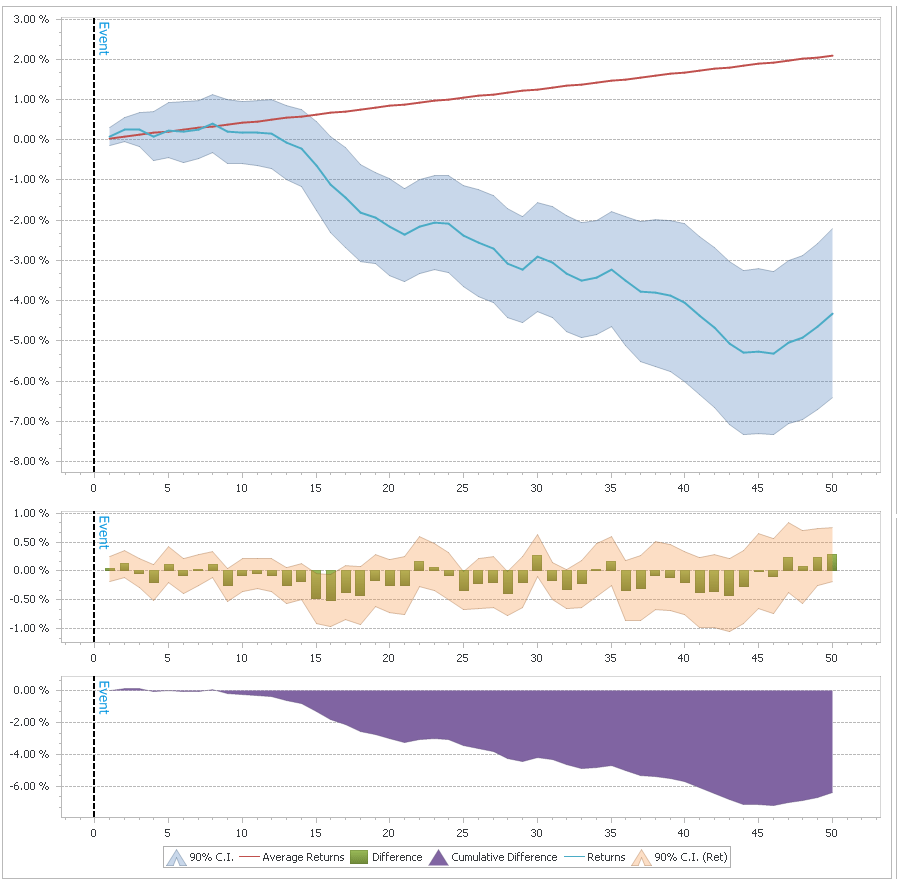
Much of this effect depends on overlapping periods, though, so it’s not as good as it looks. Still, I thinks it’s definitely something worth keeping an eye on. Of course right now we’re pretty far from that sort of signal triggering as spreads have been dropping consistently.
Size: When Small Equities Diverge
Lately we’ve been seeing the Russell 2000 (and to some extent the NASDAQ) take a dip while the S&P 500 has been going sideways with only very small drawdowns. There are several ways to formulate this situation quantitatively. I simply went with the difference between the 20-day return of SPY and IWM. The results are pretty clear: large caps outperforming is a (slightly) bullish signal, for both large and small equities.
When the ROC(20) difference is greater than 3%, SPY has above average returns for the following 2-3 weeks, to the tune of 10bp per day (IWM also does well, returning approximately 16bp per day over the next 10 days). The reverse is also useful to look at: small cap outperformance is bearish. When the ROC(20) difference goes below -3%, the next 10 days SPY returns an average -5bp per day. Obviously not enough on its own to go short, but it could definitely be useful in combination with other models.

Another interesting divergence to look at is breadth. For the last couple of weeks, while SPY is hovering around all time highs, many of the stocks in the index are below their 50 day SMAs. I’ll leave the breath divergence research as an exercise to the reader, but will note that contrary to the size divergence, it tends to be bearish.
In other news I’ve started posting binaries of QDMS (the QUSMA Data Management System) as it’s getting more mature. You can find the link on the project’s page. It’ll prompt you for an update when a new version comes out.
Read more Divergences: Yield Spreads and Size
The second, and probably final, followup to the Mining for Three Day Candlestick Patterns post. Previously, we improved performance by adding more data to the search. In this post we’ll try to improve the system further by combining multiple predictors. The central question is how to combine the forecasts. I test averaging, weighted averaging, regression, and a voting scheme and compare them against a baseline one-predictor strategy.
Set-Up
Combining predictors is a standard tactic in machine learning, but the case of k-NN predictors is a bit of an outlier. Typical ensemble methods depend on generating variations in the data set in order to generate different and complementary predictors (as in the cases of boosting and bagging). This doesn’t work very well with nearest neighbor predictors, however, because they tend to be insensitive to variations in the data set. So what can we vary? The choice of k, the choice of inputs, the choice of distance measure for the nearest neighbors, and some pre-processing options such as whether to adjust for volatility or not.
I am not going to make any variation in outputs as that’s reserved for a post of its own. The idea is pretty simple: it’s essentially a random forest with k-NN predictors instead of decision trees (here’s an interesting paper on it).
So we’re left with k, sum of absolute or sum of square distances, and volatility adjustment. I picked 10 combinations of these options:

The k values were picked at random and I’m sure it’s possible to do better by optimizing them using cross validation.
The signals obviously overlap significantly, and have similar stats when used one-by-one:

Long signal stats. Long position threshold: forecast > 5 basis points & IBS < 0.5.

Short signal stats. Short position threshold: forecast < -10 basis points & IBS > 0.5.
The instrument traded is SPY. Additional data is taken from the following instruments for the pattern search: EWY, EWD, EWC, EWQ, EWU, EWA, EWP, EWH, EWL, EFA, EPP, EWM, EWI, EWG, EWO, IWM, QQQ, EWS, EWT, and EWJ. The thresholds in each case are adjusted to result in a similar length of time spent in the market. Position sizing is done based on the 10-day realized volatility of SPY, as described in this post: leverage is equal to 20% divided by 10-day realized annualized standard deviation, with a maximum leverage of 200%. Finally, an IBS filter is applied that allows long positions only when IBS < 0.5 and short positions only when IBS > 0.5.
The baseline is the PF3 predictor: k = 75, square distance measure, no volatility adjustment. Here’s the equity curve:

PF3 predictor equity curve. $0.005 per share in commissions.
Averaging
The simplest approach is obviously to just average the 10 forecasts and then use the average value to generate trades. A long position is taken when the average forecast is greater than 15 basis points, and a short position when the average is smaller than -12.5 basis points. Here’s what the equity curve looks like:

Equity curve using average forecast. $0.005 per share in commissions.
It’s interesting to note that the dispersion of forecasts is inversely related to the accuracy of the average: the smaller the standard deviation of the forecasts, the more accurate they are. Unfortunately effect is marginal and thus not particularly useful for improving the strategy.
Weighted Averaging
A simple extension, that generates slightly better stats, is to weigh each forecast before averaging. There’s a wide array of stats one can use here (Sharpe/Sortino/MAR ratios are obvious candidates); I picked the mean square error. The inverse of the MSE becomes the forecast’s weight, so that smaller errors result in greater weights. The same thresholds as above are used to generate signals. The weights provide a slight improvement both in terms of Sharpe and MAR ratios. The equity curve:

Equity curve using weighted average forecast, with weights equal to the inverse of the mean square error. $0.005 per share in commissions.
Voting
Using a threshold for each forecast, (>5 basis points for a “long” vote, and <-10 basis points for a “short” vote), each predictor is assigned a long or short vote. The overlap between the votes is significant, between 88% and 97% for different estimators. How many votes should we require for a trade? It quickly becomes obvious that simple majority voting isn’t enough, as only near-unanimous decisions provide worthwhile predictions. The average next-day return when there are between 1 and 8 long votes is 0.4 basis points. The average return after 9 or 10 long votes is 23 basis points.
The resulting equity curve looks like this:

Equity curve using voting system. 9 or more votes required to take a position. $0.005 per share in commissions.
Ordinary Least Squares
It’s also possible to combine the forecasts using regression, with next-day returns as the dependent variable and the k-NN predictor forecasts as the independent ones.
The distribution of forecasts with OLS is very tightly clustered around 0, and for some reason higher forecasts are not associated with higher next-day returns (as they are for the 3 methods above). I don’t really understand why this is the case. The thresholds for trades are 0.5 basis points for a long trade, and -0.5 basis points for a short trade.
An issue here is, of course, multicollinearity due to the similarity of the independent variables. This can lead to, among other problems, overfitting (which is usually characterized by very large absolute values of the coefficients). Using ridge regression solves that issue by limiting the absolute value of coefficients.
A potentially interesting idea would be to constrain the coefficients to positive values, which might lessen the overfitting effects and also make much more sense on an intuitive level (after all, we know all the forecasts are similarly accurate, so negative coefficients don’t make much sense).

Equity curve using OLS regression. $0.005 per share in commissions.
Ridge Regression
If multicollinearity is a significant problem, we can use ridge regression to solve it. It offer significant improvement over the OLS approach, but it still fares badly compared to the one-predictor case. The same thresholds as in the OLS approach are used. Here’s the equity curve:

Equity curve using ridge regression. $0.005 per share in commissions.
Stats
Here are the stats for the single-predictor base case and all the combination methods:

All of them other than the voting failed horribly. I’m not sure why, but it’s good to know. The improvement provided by the voting system is sizable, however. Not only does the voting-based strategy achieve significantly higher risk-adjusted returns, it does it while spending 15% less time in the market. Those results are also easy to improve on by simply adding more predictors. The marginal gain from each new predictor will be diminishing, but there is definitely more value to wring out of it. And this is just with 3-day patterns: we can easily add 2 and 4 day patterns into the mix as well.
Other Possibilities
A wide array of machine learning methods can be used to combine predictions. Especially if the number of forecasts grew larger, techniques such as random forests or ANNs would be interesting to investigate. As long as simpler methods work very well I think there is little reason to increase the complexity (not to mention the opaqueness) of the strategy.
Read more k-NN Candlestick Pattern Search Extensions: Combining Forecasts
This is a followup to the Mining for Three Day Candlestick Patterns post. If you haven’t read the original post, do so now because I’m not going to repeat the basic mechanics of the strategy. While the approach was somewhat fruitful, it also had some obvious problems: it only seems to work in bearish or high volatility market regimes, and it couldn’t produce good short signals. The main idea I had to resolve these issues was simply to get more data.

Original strategy using only SPY data. Note long stretches of flat results.
That is easier said than done. Could we use mutual funds or index values to extend the dataset backwards? No, because the daily high/low values are inaccurate. The only alternative we are left with is using data from other instruments. So I picked a broad selection of equity ETFs to include: EWY, EWD, EWC, EWQ, EWU, EWA, EWP, EWH, EWL, EFA, EPP, EWM, EWI, EWG, EWO, IWM, QQQ, EWS, EWT, and EWJ.
The selection was comprehensive and unoptimized. I think you could do some sort of walk-forward optimization that picks the best combination of securities to include in the data set. I’m not sure how much that would help.
The additional data worked fantastically well, resolving both problems. The number of opportunities to trade increased significantly, long signals work very nicely under all market conditions, and predicting negative returns works far better. There was also an unexpected benefit: far less time is needed before the forecasts become usable. In the original implementation I waited 2000 days before starting to use the forecasts. With the extended data set this can be cut to 500, thus letting the backtest cover a longer period.
Performance-wise there were no problems, as the Accord .NET k-d tree implementation that I use is very quick. Finding the nearest 75 points in a data set of approximately 100,000, in 11 dimensions, takes less than 2 milliseconds on my overclocked 2500K.
The settings used in the search are simple: the length of the patterns is 3 days, the 75 closest ones are used to construct a forecast by averaging their next-day returns, and distance is calculated as the sum of squared distances in every dimension. Trades are taken when the forecast is above/below a certain threshold. They are then passed through a filter which only allows long positions when IBS < 0.5 and short positions only when IBS > 0.5.
It should be noted that using traditional measures of “fit” does not work very well with pattern matching. Adding the above instruments actually increases the RMSE, despite significantly increasing the trading performance of the forecasts.
A look at forecasts vs realized next-day returns:

PatternFinderMultiInput (x-axes) vs next day returns (y-axies), for IBS < 0.5 and forecast > 0
An important aspect to note is that even marginally positive forecasts work very well. For example, with the extended dataset, forecasts between 5 and 10 basis points resulted in an average 21 bp return the next day. On the other hand, using SPY data only, the return for those forecasts was just 5 basis points. What this means is that there are many more trades to take, which is what allows the strategy to do well in all market environments. Here’s the long-only equity curve:

Long position taken when IBS < 0.5 and forecast > 5 basis points. $0.005 per share in commissions.
A couple of charts to analyze the sensitivity of the long-only strategy’s results to changes in inputs (IBS limit and minimum forecast limit):

The additional data also has the benefit of making shorting possible. The equity curve doesn’t look as good, but it’s still a giant improvement over zero predictive ability on the short side:

Short position taken when IBS > 0.5 and forecast < -20 basis points. $0.005 per share in commissions.
Finally, the long and short strategies combined, along with the stats:

Long and short strategies above combined. $0.005 per share in commissions.

The concept also seems to work for stocks. For example, I tested a long-only strategy on AAPL, using the same settings as above, both with and without the addition of MSFT data. The Microsoft data improved every aspect of the results, with surprisingly consistent performance over nearly 20 years:

It would be interesting to try to apply this on a more massive scale, by increasing the data set to something like all S&P 500 stocks. Some technical restrictions prevent me from doing that right now, but I’ll come back to the idea in the future.
Read more k-NN Candlestick Pattern Search Extensions: More Data
The VXV is the VIX’s longer-term brother; it measures implied volatility 3 months out instead of 30 days out. The ratio between the VIX and the VXV captures the differential between short-term and medium-term implied volatility. Naturally, the ratio spends most of its time below 1, typically only spiking up during highly volatile times.

It is immediately obvious by visual inspection that, just like the VIX itself, the VIX:VXV ratio exhibits strong mean reverting tendencies on multiple timescales. It turns out that it can be quite useful in forecasting SPY, VIX, and VIX futures changes.
Short-term extremes
A simplistic method of evaluating short-term extremes is the distance of the VIX:VXV ratio from its 10-day simple moving average. When the ratio is at least 5% above the 10SMA, next-day SPY returns are, on average, 0.303% (front month VIX futures drop by -0.101%). Days when the ratio is more than 5% below the 10SMA are followed by -0.162% returns for SPY. The equity curve shows the returns on the long side:

Long-term extremes
When the ratio hits a 200-day high, next-day SPY returns have been 0.736% on average. Implied volatility does not fall as one might expect, however.
More interestingly, the picture is reversed if we look at slightly longer time frames. 200-day VIX:VXV ratio extremes can predict pullbacks in SPY quite well. The average daily SPY return for the 10 days following a 200-day high is -0.330%. This is naturally accompanied by increases in the VIX of 1.478% per day (the front month futures show returns of 1.814% per day in the same period). It’s not a fail-proof indicator (it picked the bottom in March 2011), but I like it as a sign that things could get ugly in the near future. We recently saw a new 200-day high on the 19th of December: since then SPY is down approximately 1%.

This is my last post for the year, so I leave you with wishes for a happy new year! May your trading be fun and profitable in 2013.
Read more The VIX:VXV Ratio
Introduction
A quick intro to VIX ETPs (some are ETFs, others are ETNs) before we get to the meat: the VIX itself is not tradable, only futures on the VIX are. These futures do not behave like equity index futures which move in lockstep with the underlying, for a variety of reasons. A way to get exposure to these futures without holding them directly, is by using one or more VIX futures-based ETPs. These come in many varieties (long/short, various target average times to expiration, various levels of leverage).
The problem with them, and the reason they fail so badly at mirroring movements in the VIX, is that they have to constantly roll over their futures holdings to maintain their target average time to expiration. A 1-month long ETP will be selling front month futures and buying 2nd month futures every day, for example. Front month futures are usually priced lower than 2nd month futures, which means that the ETP will be losing value as it makes these trades (it’s selling the cheap futures and buying the expensive ones), and vice versa for short ETPs. This amounts to a transfer of wealth from hedgers to speculators willing to take opposite positions; this transfer can be predicted and exploited.
I’ll be looking at two such VIX futures-based instruments in this post: VIXY (which is long the futures), and XIV (which is short the futures). As you can see in the chart below, while the VIX is nearly unchanged over the period, VIXY has lost over 80% of its value. At the same time, XIV is up 50% (though it did suffer a gigantic drawdown).

There are many different approaches to trading these ETPs (for example Mike Brill uses realized VIX volatility to time his trades). The returns are driven by the complex relationships between the value of the index, the value of the index in relation to its moving average, the value of the futures in relation to the index, and the value of various future maturities in relation to each other. These relationships give rise to many strategies, and I’m going to present two of them below.
I’ll be using different approaches for the long and short sides of the trades. Short based on the ratio between the front and 2nd month contract, and long using the basis. Here are the rules:
Go long XIV at close (“short”) when:
- 2nd month contract is between 5% and 20% higher than the front month contract.
Go long VIXY at close (“long”) when:
- Front month future is at least 2.5% below the index.
Finally, if both of the above conditions are triggered, go to cash.
Results
First let’s have a look at how these strategies perform without the hedge. Using data from January 2011 to November 2012, here are the daily return stats for these two approaches individually and when combined:

Equity curves & drawdowns:

The biggest issues with VIX ETN strategies are large drawdowns, and large sudden losses when the VIX spikes up (and to a lesser extent when it spikes down; these tend to be less violent though). A spike in implied volatility is almost always caused by large movements in the underlying index, in this case the S&P 500. We can use this relationship in our favor by utilizing SPY as a hedge.
- When long XIV, short SPY in an equal dollar amount.
- When long VIXY, go long SPY in an equal dollar amount.
The stats:

And the equity curves & drawdowns:

The results are quite good. The bad news is that we have to give up about 40% of CAGR. On a risk-adjusted basis, however, returns are significantly improved.
- CAGR / St. Dev. goes from 38.7 to 45.9.
- CAGR / Max Drawdown goes from 4.5 to 4.9.
All risk measures show significant improvement:
- The worst day goes from a painful -12% to a manageable -9%.
- Maximum drawdown goes from -36.5% to -25.7%.
- Daily standard deviation goes from 4.28% to 2.76%.
Of course, just because risk-adjusted returns are improved does not mean it’s necessarily a good idea. Holding SPY results in both direct costs (commissions, slippage, shorting costs) as well as the opportunity cost of the capital’s next-best use. The improvement may not be enough to justify taking away capital from another system, for example.
Another possibility would be to implement this idea using options, which have the benefit of requiring a small outlay. Especially when holding XIV, SPY puts could be a good idea as both implied volatility and price would move in our direction when the VIX spikes up. However, this must be weighted against theta burn. I don’t have access to a dataset for SPY options to test this out, unfortunately (anyone know where I can get EOD options data that is not absurdly expensive?).
If you want to play around with the data yourself, you can download the spreadsheet here.
Footnotes
Read more Hedging VIX ETP Strategies Using SPY
UPDATE: read The IBS Effect: Mean Reversion in Equity ETFs instead of this post, it features more recent data and deeper analysis.
The location of the closing price within the day’s range is a surprisingly powerful predictor of next-day returns for equity indices. The closing price in relation to the day’s range (or CRTDR [UPDATE: as reader Jan mentioned in the comments, there is already a name for this: Internal Bar Strength or IBS] if you’re a fan of unpronounceable acronyms) is simply calculated as such:

It takes values between 0 and 1 and simply indicates at which point along the day’s range the closing price is located. In this post I will take a look not only at returns forecasting, but also how to use this value in conjunction with other indicators. You may be skeptical about the value of something so extremely simplistic, but I think you’ll be pleasantly surprised.
The basics: QQQ and SPY
First, a quick look at QQQ and SPY next-day returns depending on today’s CRTDR:


A very promising start. Now the equity curves for each quartile:


That’s quite good; consistency through time and across assets is important and we’ve got both in this case. The magnitude of the out-performance of the bottom quartile is very large; I think we can do something useful with it.
There are several potential improvements to this basic approach: using the range of several days instead of only the last one, adjusting for the day’s close-to-close return, and averaging over several days are a few of the more obvious routes to explore. However, for the purposes of this post I will simply continue to use the simplest version.
CRTDR Internationally
A quick look across a larger array of assets, which is always an important test (here I also incorporate a bit of shorting):

Long when CRTDR < 45%, short when CRTDR > 95%. $10k per trade. Including commissions of $0.005 per share, excluding dividends.
One question that comes up when looking at ETFs of foreign indices is about the effect of non-overlapping trading hours. Would we be better off using the ETF trading hours or the local trading hours to determine the range and out predictions? Let’s take a look at the EWU ETF (iShares MSCI United Kingdom Index Fund) vs the FTSE 100 index, with the following strategy:
- Go long on close if CRTDR < 45%
- Go short on close if CRTDR > 95%

FTSE vs EWU CRTDR strategy, 1996-2012. $1m per trade (the number was a technical necessity due to the price of the FTSE 100 index).
Fascinating! This result left me completely stumped. I would love to hear your ideas about this…I have a feeling that there must be some sort of explanation, but I’m afraid I can’t come up with anything realistic.
Trading Signal or Filter?
It should be noted that I don’t actually use the CRTRD as a signal to take trades at all. Given the above results you may find this surprising, but all the positive returns are already captured by other, similar (and better), indicators (especially short-term price-based indicators such as RSI(3)). Instead I use it in reverse: as a filter to exclude potential trades. To demonstrate, let’s have a look at a very simplistic mean reversion system:
- Buy QQQ at close when RSI(3) < 10
- Sell QQQ at close when RSI(3) > 50
On average, this will result in a daily return of 0.212%. So we have two approaches in our hands that both have positive expectancy, what happens if we combine them?
- Go long either on the RSI(3) criteria above OR CRTDR < 50%

RSI(3) and RSI(3) w/ CRTDR strategy applied to QQQ. Commissions not included.
This is a bit surprising: putting together two systems, both of which have positive expectancy, results in significantly lower returns. At this point some may say “there’s no value to be gained here”. But fear not, there are significant returns to be wrung out of the CRTDR! Instead of using it as a signal, what if we use it in reverse as a filter? Let’s investigate further: what happens if we split these days up by CRTDR?

Now that’s quite interesting. Combining them has very bad results, but instead we have an excellent method to filter out bad RSI(3) trades. Let’s have a closer look at the interplay between RSI(3) signals and CRTDR:

Next-day QQQ returns.
And now the equity curves with and without the CRTDR < 50% filter:

RSI(3) and RSI(3) w/ CRTDR < 50% filter applied to QQQ. Commissions not included.
That’s pretty good. Consistent performance and out-performance relative to the vanilla RSI(3) strategy. Not only that, but we have filtered out over 35% of trades which not only means far less money spent on commissions, but also frees up capital for other trades.
UPDATE: I neglected to mention that I use Cutler’s RSI and not the “normal” one, the difference being the use of simple moving averages instead of exponential moving averages. I have also uploaded an excel sheet and Multicharts .net signal code that replicate most of the results in the post.
Read more Closing Price in Relation to the Day’s Range, and Equity Index Mean Reversion
Can extreme changes in implied volatility help predict future returns? And can we use a VIX surrogate as a substitute? First, let’s take a look at the WVF and its relationship to the VIX.
The Williams’ VIX Fix (WVF) is an indicator meant to roughly approximate the VIX. It can be useful in situations where there is no implied volatility index for the instrument we want to trade. The WVF is simply a measure of the distance between today’s close and the 22-day highest close; it is calculated as follows:

A quick visual comparison between the VIX and WVF:

The WVF and VIX behave similarly during volatility spikes, but the WVF fails to emulate the VIX when it hovers at relatively low values. The correlation coefficient between VIX and WVF returns is 0.62, while regressing VIX returns on WVF returns using OLS results in an R2 statistic of 0.38.
We’re not going to be using the level of the VIX and WVF (hardcoding strategies to specific levels of the VIX is generally a terrible idea), so the above chart is somewhat useless for our purposes; we’re going to be looking at the 100-day percentile rank of the daily change. Here is a comparison over a couple of recent months:

Some times they move in lockstep, other times there seems to be almost no relation between them. Still, for such a simple indicator, I would say that the WVF does a fantastic job at keeping up with the VIX.
As you probably know, (implied) volatility is highly mean reverting. Extreme increases in the VIX tend to be followed by decreases. These implied volatility drops also tend to be associated with positive returns for equities. Let’s take a look at simple strategy to illustrate the point:
- Buy SPY on close if the VIX percentage change today is the highest in 100 days.
- Sell on the next close.
Here’s the equity curve and stats:

Nothing spectacular, but quite respectable. Somewhat inconsistent at times of low volatility, but over the long term it seems to be reliable. What about the same approach, but using the WVF instead?

The WVF outperforms the VIX! A somewhat surprising result…the equity curves look similar of course, with long periods of stagnation during low volatility times. Over the long term the stats are quite good, but we might be able to do better…
There is surprisingly little overlap between the VIX and WVF approaches. There are 96 signals from VIX movements, and 109 signals from WVF movements; in 48 instances both are triggered. These 48 instances however are particularly interesting. Here’s a quick breakdown of results depending on which signal has been triggered:

Now this is remarkable. Despite performing better on its own, when isolated the VIX signal is completely useless. This is actually a very useful finding and extends to other similar situations: extreme volatility alone is not enough for an edge, but if used in combination with price-based signals, it can provide significant returns. I leave further combinations on this theme as an exercise for the reader.
A look at the equity curve of “both”:

Long SPY when VIX % change and WVF change are both the highest of the last 100 days, $100k per trade, 1993-2012, no commissions or dividends.
Now that’s just beautiful. You may say “but 37% over 20 years isn’t very impressive at all!”. And you’re right, it isn’t. But for a system that spends almost 99% of the time in cash, it’s fantastic. Want more trade opportunities? Let’s see what happens if we relax the limits on “extremeness”, from the 99th percentile through to the 75th:

Net profit increases, but profitability per trade, and most importantly risk-adjusted returns suffer. The maximum drawdown increases at a much faster rate than net profits if we relax the limits. Still, there could be value in using even the 50th percentile not as a signal in itself, but (like the day of the month effects) as a slight long bias.
Finally, what if we vary the VIX and WVF limits independently of each other? Let’s have a cursory look at some charts:

As expected, the profit factor is highest at (0.99, 0.99), while net profits are highest at the opposite corner of (0.75, 0.75). It’s interesting to note however, that drawdown-adjusted returns are roughly the same both along the (0.99, 0.75-0.99) and (0.75-0.99, 0.99) areas; as long as one of the two is at the highest extremes, you can vary the other with little consequence in terms of risk-adjusted returns, while increasing net profits. This is definitely an area deserving of further analysis, but that’s for another post.
That’s it for now; I hope some of these ideas can be useful for you. In part 2 we’ll take a look at how the above concepts can be applied to international markets, where there is no direct relation to the VIX and there are no local implied volatility indices to use.
Footnotes
Read more Equity Returns Following Extreme VIX and WVF Movements, Part 1
Today the S&P 500 closed at a 20-day low. Is there anything useful we can do with this piece of information? Let’s take a look at the performance of SPY after it closes at a 20-day low:

Not particularly useful I’m afraid, just random variations around the average. What about other look-back lengths?

Now this is more interesting. 60-day lows and up appear to have a bit of an edge, both for the day immediately after the low, as well as the medium term afterwards.
Let’s take a closer look at the returns after a 200-day low, with 95% confidence interval bands around them. Naturally, returns tend to be highly volatile around 200-day lows, which (combined with the small number of observations) means a very wide confidence interval.

The 200-day low effect also seems to be prevalent in most equity indices, but without the regularity and strength that has been displayed by the S&P 500. Finally, what about new highs?

Nothing to see here, move along! Slight underperformance compared to the average, but nowhere near enough to even consider shorting.
Read more S&P 500 Returns Following New Lows (and Highs)
Rummaging through my bottomless “TO DO” list, I found this little comment:
# of up/dn days in period, then re-scale that using percentrank….with net % move?
An interesting way to spend Sunday afternoon, and another blog post!
After playing around with the concept for a while, I ended up creating a simple indicator that, as it turns out, is impressively good at picking out bottoms, and has very strong 1-day and acceptable medium-term predictive power. In an attempt to come up with the most awkward-sounding acronym possible, I decided on the name “Up/Down and Intensity Day Summation Rank Indicator”, or UDIDSRI. Here’s what I did:
The first iteration
I started out with a very simple concept:
- If the day closes up, movement = 1, otherwise movement = -1.
- Sum movement over the last 20 days.
- UDIDSRI is the % rank of today’s sum, compared to the last 50 days of sums.
The case that presents the most interest is when UDIDSRI is equal to zero (i.e. the lowest value in 50 days), and we’ll have a look at how this works further down. I felt that this indicator could be significantly improved by adding a bit of nuance. Not all down days are equal, so I thought it would be a good idea to take into account the magnitude of the moves as well as their direction.
The second iteration
The second version of the algorithm:
- If the day closes up, movement = 1, otherwise movement = -1.
- Multiply movement by (1 +abs( return))5
- Sum the movements for the last 20 days.
- UDIDSRI is the % rank of today’s sum, compared to the last 50 days of sums.
The choice of the 5th power is completely arbitrary and un-optimized (as are the 20-day summation, and 50-day ranking) and can probably be optimized for better performance.
Here’s a chart comparing the two versions on the last few months of SPY (yellow is 1st iteration, red is 2nd):

You can clearly see that the 2nd iteration doesn’t like to stay at 0 for so long, and tends to respond a bit faster to movements. As such, the 2nd iteration gives far fewer signals, but they’re of much higher quality. I’ll be using the 2nd version for the rest of this post.

Note that this approach is completely useless for going short. The indicator hitting its maximum value provides no edge either for mean reversion or trend following.
A quick test around the globe to make sure I wasn’t curve fitting:

That turned out rather well…
Thus far we have only looked at the short-term performance of UDIDSRI. Let’s see how it does over the medium term after hitting 0:

There seems to be a period of about 30 trading days after UDIDSRI hits 0, during which you can expect above-average returns. Let’s take a look at a strategy that crudely exploits this:
- Buy SPY at close if UDIDSRI = 0.
- Use a 2% trailing stop (close-to-close) to exit.
The trailing stop makes us exit quickly if we haven’t entered at a bottom, but stays with the trend if the entry is good. Here are the stats and equity curve for this strategy applied to SPY, using $100k per trade, without commissions or slippage:


Finally here are some trades this strategy would have taken in 2011 and early 2012:

The most significant problem with the tight trailing stop is that it exits at pullbacks instead of tops (which is particularly painful during heavy bear markets), so one easy improvement would be to add an indicator for over-extension and use that to time the exit. But I’ll leave that as homework.
All in all I’m quite satisfied with the UDIDSRI. I was really surprised at how it manages to pick bottoms with such accuracy, and I will definitely add it to the repertoire of signals that I use for swing trading.
If you want to play with the UDIDSRI yourself, I have uploaded an excel worksheet as well as the indicator and signal for MultiCharts .NET.
Footnotes
Read more The Predictive Value of the Number and Magnitude of Recent Up/Down Days: UDIDSRI




























































